| 第一胎 | 第二胎 | 第三胎 | 第四胎 | |
| 1 | ♀ | ♀ | ♀ | ♀ |
| 2 | ♀ | ♀ | ♀ | ♂ |
| 3 | ♀ | ♀ | ♂ | ♀ |
| 4 | ♀ | ♀ | ♂ | ♂ |
| 5 | ♀ | ♂ | ♀ | ♀ |
| 6 | ♀ | ♂ | ♀ | ♂ |
| 7 | ♀ | ♂ | ♂ | ♀ |
| 8 | ♀ | ♂ | ♂ | ♂ |
| 9 | ♂ | ♀ | ♀ | ♀ |
| 10 | ♂ | ♀ | ♀ | ♂ |
| 11 | ♂ | ♀ | ♂ | ♀ |
| 12 | ♂ | ♀ | ♂ | ♂ |
| 13 | ♂ | ♂ | ♀ | ♀ |
| 14 | ♂ | ♂ | ♀ | ♂ |
| 15 | ♂ | ♂ | ♂ | ♀ |
| 16 | ♂ | ♂ | ♂ | ♂ |
生幾個男孩幾個女孩的機率
如果生男生女的機會一樣,叔叔家有4個小孩,全都是女孩的機會大不大?有1個男孩和3個女孩的機會,與有3個男孩和1個女孩的機會一樣嗎?
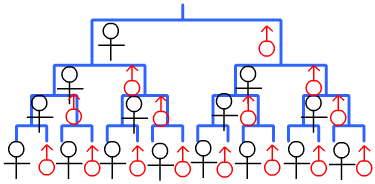
一般用樹狀圖來討論,如附圖。♀表示女生,♂表示男生,叔叔的四個小孩的可能性別如下表:
 |
|
總有16種可能結果,其中4個孩子都是女生只有1個可能︰(16),所以4個孩子都是女生的機率是$\frac{1}{16}$。
1個男孩和3個女孩有4個可能︰(2)(3)(5)(9),所以1個男孩和3個女孩的機率是$\frac{4}{16}$。
3個男孩和1個女孩有4個可能︰(8)(12)(14)(15),所以3個男孩和1個女孩的機率是$\frac{4}{16}$。
因此,有1個男孩和3個女孩的機會,與有3個男孩和1個女孩的機會是一樣的。
帕斯卡在1654年發表帕斯卡三角,即自然數冪方的二項展開式的係數。1664~1665年期間牛頓將二項式的展開式推廣到有理數冪方, 雅各布·白努利(Jacob Bernoulli ,1654-1705)提出二項試驗和二項分布。
$\small\left( \begin{array}{} n \\ m \end{array} \right) $pm(1-p)n-m =$\large\frac{n!}{m!(n-m)!}$pm(1-p)n-m 。
如果生男的機率是p,生女的機率是1-p=q,則生下2個孩子的男女機率=(p+q)2=$\small\left( \begin{array}{} 2 \\ 0 \end{array} \right) $p0q2+$\small\left( \begin{array}{} 2 \\ 1 \end{array} \right) $pq+$\small\left( \begin{array}{} 2 \\ 2 \end{array} \right) $p2q0=q2+2pq+p2。包含生二男的機率p2,一男一女的機率=pq+qp=2pq,生二男的機率q2。
生下3個孩子的男女機率=(p+q)3=$\small\left( \begin{array}{} 3 \\ 0 \end{array} \right) $p0q3+$\small\left( \begin{array}{} 3 \\ 1 \end{array} \right) $pq2+$\small\left( \begin{array}{} 3 \\ 2 \end{array} \right) $p2q+$\small\left( \begin{array}{} 3 \\ 3 \end{array} \right) $p3q0=q3+3q2p+3qp2+p3。包含生三男的機率p3,二男一女的機率=3p2q,生一男二女的機率3pq2,生三女的機率q3。
假設生n個孩子,其中m個男生的機率=$\small\left( \begin{array}{} n \\ m \end{array} \right) $pmqn-m。
帕斯卡三角

如果生下4個孩子且如果生男生女的機率都是$\frac{1}{2}$。由上往下的第4列數字分別是1、4、6、4、1。
數字相加,1+4+6+4+1=16,就是生4個小孩的性別的可能結果數。
左邊第1個數字是 1,表示生4個男孩的機率是$\frac{1}{16}$。即$\small\left(
\begin{array}{} 4 \\ 4\end{array} \right)$($\large\frac{1}{2}$)4($\large\frac{1}{2}$)0
左邊數來第2個數字是4,它表示 3個男孩和1 個女孩的機率是$\frac{4}{16}$。即$\small\left(
\begin{array}{} 4 \\ 3 \end{array} \right)$($\large\frac{1}{2}$)3($\large\frac{1}{2}$)
左邊數來第3個數字是6,它表示2個男孩和2個女孩的機率是$\frac{6}{16}$。即$\small\left(
\begin{array}{} 4 \\ 2 \end{array} \right)$($\large\frac{1}{2}$)2($\large\frac{1}{2}$)2
左邊數來第4個數字是4,它表示 1個男孩和3個女孩的機率是$\frac{4}{16}$。即$\small\left(
\begin{array}{} 4 \\ 1 \end{array} \right)$($\large\frac{1}{2}$)($\large\frac{1}{2}$)3
左邊數來第5個數字是1,它表示 4個女孩的機率是$\frac{1}{16}$。即$\small\left(
\begin{array}{} 4 \\ 0 \end{array} \right)$($\large\frac{1}{2}$)0($\large\frac{1}{2}$)4。
Copyright ©昌爸工作坊 all rights reserved.