比較三種平均數

比較 A.M、G.M、H.M
　

a和b兩數，其算術平均數(A.M)、幾何平均數(G.M)、調和平均數(H.M)分別如下：

A.M=$\large\frac{a+b}{2}$，G.M=$\sqrt{ab}$，H.M=$\large\frac{2ab}{a+b}$=$\large\frac{2}{\frac{1}{a}+\frac{1}{b}}$。

如果a和b都是正數，則

( $\sqrt{a}-\sqrt{b}$ )²≧ 0，

$a-2\sqrt{ab}+b $ ≧ 0，

因此$\large\frac{a+b}{2}$ ≧ $\sqrt{ab}$，即 A.M ≧ G.M。

( $\large\frac{1}{\sqrt{a}}-\frac{1}{\sqrt{b}}$ )²≧ 0，

$\large\frac{1}{a}-\frac{2}{\sqrt{ab}}+\frac{1}{b}$≧ 0，

$\large\frac{1}{a}+\frac{1}{b}$≧ $\large\frac{2}{\sqrt{ab}}$，

因此$\sqrt{ab}$ ≧ $\large\large\frac{2}{\large\frac{1}{a}+\large\frac{1}{b}}$=$\large\frac{2ab}{a+b}$，即 G.M ≧ H.M。

所以算術平均數(A.M) ≧ 幾何平均數(G.M) ≧ 調和平均數(H.M)。

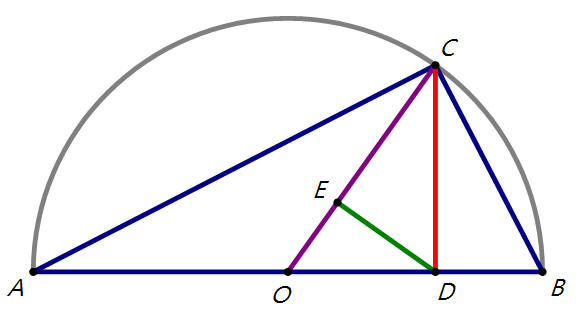
圓O直徑AB，C點在圓周，CD⊥AB，D點是垂足；DE⊥OC，E點是垂足。

假設AD=a，DB=b，則 OC=$\large\frac{a+b}{2}$。

由母子相似性質知CD²=AD ×DB = ab，所以CD=$\sqrt{ab}$。

由母子相似性質知CD²=CE ×CO ，即ab=CE ×$\large\frac{a+b}{2}$，所以CE=$\large\frac{2ab}{a+b}$。

由附圖知OC > CD > CE，所以$\large\frac{a+b}{2}$ > $\sqrt{ab}$ > $\large\frac{2}{\frac{1}{a}+\frac{1}{b}}$。