| x | 9x | 9x | 9x |
| 1 | 9 | 10-1 | $\large\frac{10^2(10^0-1)}{9}$+(10-1) |
| 12 | 108 | 102+10-2 | $\large\frac{10^2(10^1-1)}{9}$+(10-2) |
| 123 | 1107 | 103+102+10-3 | $\large\frac{10^2(10^2-1)}{9}$+(10-3) |
| 1234 | 11106 | 104+103+102+10-4 | $\large\frac{10^2(10^3-1)}{9}$+(10-4) |
| 12345 | 111105 | 105+104+103+102+10-5 | $\large\frac{10^2(10^4-1)}{9}$+(10-5) |
| 123456 | 11111104 | 106+105+104+103+102+10-6 | $\large\frac{10^2(10^5-1)}{9}$+(10-6) |
| 1234567 | 111111103 | 107+106+105+104+103+102+10-7 | $\large\frac{10^2(10^6-1)}{9}$+(10-7) |
| 12345678 | 1111111102 | 108+107+106+105+104+103+102+10-8 | $\large\frac{10^2(10^7-1)}{9}$+(10-8) |
| 123456789 | 11111111101 | 109+108+107+106+105+104+103+102+10-9 | $\large\frac{10^2(10^8-1)}{9}$+(10-9) |
| $\large\frac{10^2(10^{n-1}-1)}{9}$+(10-n) | |||
| n $\in${ 1，2，3，4，5，6，7，8，9 } | |||
$\frac{\Large\frac{10^2(10^{n-1}-1)}{9}+\large (10-n)}{9}$=$\frac{\large 10^2(10^{n-1}-1)+9(10-n)}{81}$=$\frac{\large 10^{n+1}-9n-10}{81}$，n $\in${ 1，2，3，4，5，6，7，8，9 }
令 f(x)=$\frac{\large 10^{x+1}-9x-10}{81}$，x$\in${ 1，2，3，4，5，6，7，8，9 }
| x | f(x) |
| 1 | 1 |
| 2 | 12 |
| 3 | 123 |
| 4 | 1234 |
| 5 | 12345 |
| 6 | 123456 |
| 7 | 1234567 |
| 8 | 12345678 |
| 9 | 123456789 |
f(x)=$\frac{\large 10^{x+1}-9x-10}{81}$，x$\in${0，-1，-2，-3，-4，-5，-6，-7，-8，-9，-10 }
| x | f(x) |
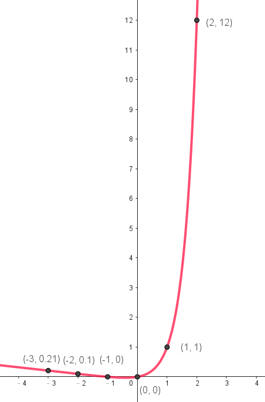
| 0 | 0 |
| -1 | 0 |
| -2 | 0.1 |
| -3 | 0.21 |
| -4 | 0.321 |
| -5 | 0.4321 |
| -6 | 0.54321 |
| -7 | 0.654321 |
| -8 | 0.7654321 |
| -9 | 0.87654321 |
| -10 | 0.987654321 |
美國加州高中學生Derek Hollowood 發現這個函數，所以此函數用他的名字來命名。
Copyright © 昌爸工作坊 all rights reserved.