哥尼斯堡七橋問題（Seven Bridges of
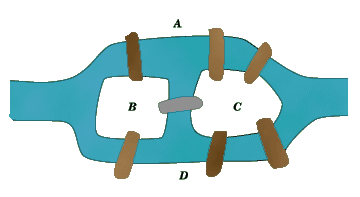
Königsberg）是圖論的著名問題。這個問題衍生自古東普魯士的哥尼斯堡（今俄羅斯加里寧格勒）市區跨在普列戈利亞河的兩岸，河中有兩座小島，小島和河的兩岸靠七座橋連接。試想如何走一遍七座橋且不重複路徑？用點線將地景簡化成下圖，A、B、C、D四點視作四個區域，而將連接兩點間的線視作橋樑。轉換原來問題成為「是否用一筆畫過這七座橋，而不重複路徑」。
哥尼斯堡的七座橋
哥尼斯堡七橋問題（Seven Bridges of
Königsberg）是圖論的著名問題。這個問題衍生自古東普魯士的哥尼斯堡（今俄羅斯加里寧格勒）市區跨在普列戈利亞河的兩岸，河中有兩座小島，小島和河的兩岸靠七座橋連接。試想如何走一遍七座橋且不重複路徑？
用點線將地景簡化成下圖，A、B、C、D四點視作四個區域，而將連接兩點間的線視作橋樑。轉換原來問題成為「是否用一筆畫過這七座橋，而不重複路徑」。
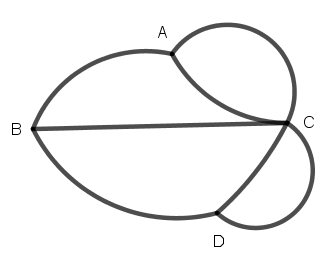
尤拉研究一筆畫問題，他稱線的匯合點為頂點。如果偶數線匯合在一個頂點，稱之為偶頂點;如果奇數線匯合在一個頂點，則稱之為奇頂點。他證明：「如果整個線網沒有奇頂點或只有兩個奇頂點，就可以一筆畫過全部的路徑。」也就是說，線網有3個以上(含3個)奇頂點，就不能一筆畫。(線網不可能只有一個奇頂點)
現在，你再想想看，一個人是否能走一遍七座橋且不重複路徑呢？
Copyright © 昌爸工作坊 all rights reserved.