4正方形

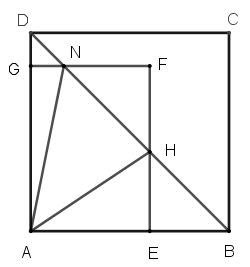
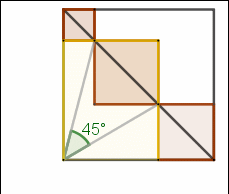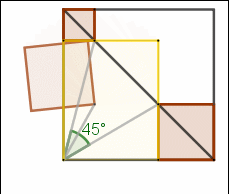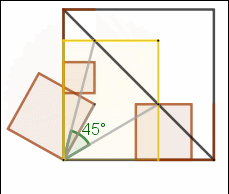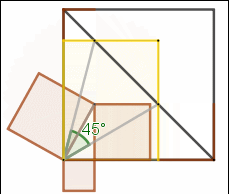
已知長方形AEFG的面積是正方形ABCD的一半，正方形ABCD對角線DB和長方形AEFG相交於N、H點。
那麼，∠NAH大小是否是一定值?

假設正方形ABCD的邊長是a，面積是a²。長方形AEFG的面積是$\large\frac{a^2}{2}$，如果AE=b，則AG=$\large\frac{a^2}{2b}$。
因為等腰直角三角形ABD，且GN//AB，HE//DA，所以DG=GN且HE=EB。
因為AE=b，AG=$\large\frac{a^2}{2b}$，所以BE=a-b=HE，DG=a-$\large\frac{a^2}{2b}$=GN。
假設∠HAE=α，∠NAG=β，則tanα=$\frac{\overline{HE}}{\overline{AE}}$=$\large\frac{a-b}{b}$=$\large\frac{a}{b}$-1，因為tanβ=$\frac{\overline{GN}}{\overline{AG}}$=$\small\displaystyle\frac{a-\displaystyle\small\frac{a^2}{2b}}{\displaystyle\small\frac{a^2}{2b}}$=$\large\frac{2b}{a}$-1。
所以tan(α+β)=$\displaystyle\small\frac{tanα+tanβ}{1-tanα tanβ}$=$\small\frac{\displaystyle\small\frac{a}{b}+\displaystyle\small\frac{2b}{a}-2}{\large 1-(3-\displaystyle\small\frac{a}{b}-\displaystyle\small\frac{2b}{a})}$=1，所以α+β=45°，因此∠NAH=(90-45)°=45°。
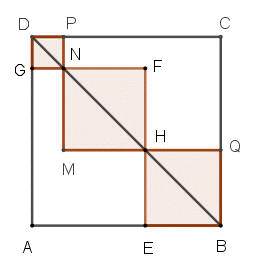
此外，因為GN=$a-\large\frac{a^2}{2b}$，BE=a-b，NF=b-(a-$\large\frac{a^2}{2b}$)，且$\small\overline{NF}^{2}$=b²-2b(a-$\frac{a^2}{2b}$)+(a-$\frac{a^2}{2b}$)²=(b-a)²+(a-$\frac{a^2}{2b}$)²=$\small\overline{BE}^{2}+\overline{GN}^{2}$。

所以正方形NFHM面積=正方形DPNG面積+正方形HQBE面積。

相關連結︰4正方形(ggb)

Copyright ©昌爸工作坊 All Rights Reserved.