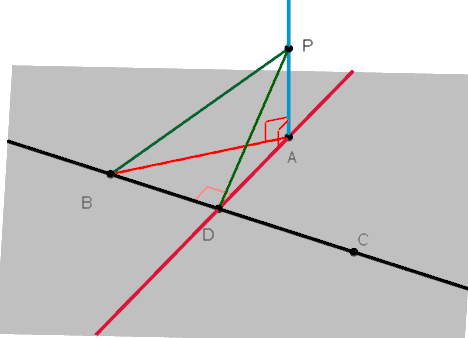
三垂線定理

直線$\overleftrightarrow{BD}$在平面E，若P點不在平面E，如何判別直線$\overleftrightarrow{PD}$是否垂直於直線$\overleftrightarrow{BD}$?

「如果PD在平面E的正投影AD垂直於直線$\overleftrightarrow{BD}$，則PD垂直於BD。」

三垂線定理︰
「已知A點在平面E，且直線$\overleftrightarrow{PA}$垂直於平面E。直線$\overleftrightarrow{BD}$在平面E，不經過A點。若直線$\overleftrightarrow{AD}$和直線$\overleftrightarrow{BD}$垂直，則PD垂直於直線$\overleftrightarrow{BD}$。」

因為直線$\overleftrightarrow{PA}$垂直於平面E，所以PA⊥AD且PA⊥AB，因此△PAD和△PAB都是直角三角形，

PD和PB是斜邊長，得 PD²=PA²+ AD²...(1)， PB²=PA²+ AB²...(2)。

(1)-(2) PD²-PB²= AD²- AB²，得 AB²= AD² - PD²+PB²...(3)。

如果AD⊥BD ，則 AB²=AD²+ DB²...(4)

由(4)-(3) 得 PB²= PD² +DB²，所以△PDB是直角三角形，PB的對角是直角，即PD⊥BD 。

相關網頁︰三垂線定理ggb