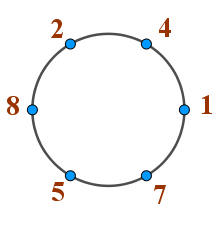
142857

142857×1=142857，142857×2=285714，142857×3=428571，142857×4=571428，

142857×5=714285，142857×6=857142，142857×7=999999。

14+28+57=99，142+857=999，且 1+4+2+8+5+7=27，2+7=9。

1÷7=0.142857 ，2÷7=0.285714 ，3÷7=0.428571 ，4÷7=0.571428 ，

5÷7=0.714285 ，6÷7=0.857142 ，7÷7=0.9 。

為什麼7÷7=0.9 而不是7÷7=1，其實1=0.9 。

因為0.9 = 9×0.1 =9×(0.1+0.01+0.001+......) =
$$9 \times \lim_{n\to\infty} \frac{0.1(1-0.1^n)}{1-0.1}=\frac{0.9}{0.9}=1$$

數學家高斯提過一個問題︰「是否有無窮多個質數 p，使得$\frac{1}{p}$的循環節是 p-1位。」

例如:

p=7，$\frac{1}{7}$=0.142857，循環節142857是6位。

p=17，$\frac{1}{17}$=0.5882352941176470 ，循環節5882352941176470是16位。

p=19，$\frac{1}{19}$=0.526315789473684210 ，循環節5882352941176470是18位。

如果黎曼假設The Riemann Hypothesis 成立，那麼高斯的問題就成立。
　