落網--球台數學

名詞定義：

1. [m：n] 表示長、寬分別是m.、n的桌面，其中m＞n，而且是正整數。

2. T[m：n] 表示撞球和桌邊的碰撞次數。

3. S[m：n] 表示撞球經過的方格數目。

4. P[m：n] 表示撞球直線路徑數。

5. 桌面右上角、右下角、左上角分別記作ru、rd、lu。

6. 併合：如果S[m：p]＋S[m：q]＝S[m：p+q]，而且S[m：p]和S[m：p+q]落網桌角同。
   或S[m：p]＋S[n：p]＝S[m+n：p]，而且S[m：p]和S[m+n：p]落網桌角同。稱為可併和。記作[m：p]＋[m：q]＝[m：p+q]，或[m：p]＋[n：p]＝[m+n：p]。

7. 拆離：如果S[m：p]－S[m：q]＝S[m：p－q]，而且S[m：p]和S[m：p－q]落網桌角同。或S[m：p]－S[n：p]＝S[m－n：p]，而且S[m：p]和S[m－n：p]落網桌角同。稱為可拆離。記作[m：p]－[m：q]＝[m：p－q]，或[m：p]－[n：p]＝[m－n：p]。

   作品摘要

1. T[m：n]=0

2. 如果(m，n)=1，則T[m，n]=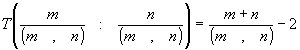m＋n－2

3. 如果(m，n)≠1，則T[m，n]=

4. m、n是正整數，則T[m，n]=

5. P[m：n]= T[m：n]+1

6. 如果球經桌面所有方格後落網，則S[m：n]＝m×n。反之亦然。

7. [m：m-1]球落網前，S[m：m-1]＝m×(m＋1)

8. 如果(m，n)=1，則S[m：n]＝m×n

9. 如果(m，n) ≠1，則S[m：n]＝[m，n]

10. 如果(m，n)=1，球經所有方格後落網。

11. 如果P[m：n]是偶數，球進rd或lu。如果P[m：n]是奇數，球進ru。

12. 如果m是奇數，是偶數，球進lu。

13. 如果m是偶數，n是奇數，則球進rd。

14. 如果m和n都是奇數，球進ru。

15. 如果m和n是偶數，是偶數，則球進rd。
    如果m和n是偶數，是偶數，則球進lu。
    如果m＝n，則球進ru。

16. 如果是偶數，則球進rd。如果是偶數，則球進lu。如果和是奇數，則球進ru。

17. 如果(m，p)=(m，q)=(m，p+q)=1，p和p+q同為偶數或奇數，則[m：p]＋[m：q]＝
    [m：p+q]。

18. 如果m是偶數，則[m：p]和[m：q]不可併合。

19. 如果(m，p)=(m，q)=(m，p+q)=1，q是偶數，則[m：p]＋[m：q]＝[m：p+q]。

20. 如果m是大於2的質數，q是偶數且m＞p+q，則[m：p]＋[m：q]＝[m：p+q]。

21. 如果(m，p)=(n，p)=(m+n，p)=1，m和m+n同為偶數或奇數，則[m：p]＋[n：p]＝[m+n：p]。

22. 如果p是偶數，則[m：p]和[n：p]不可併合。

23. 如果(m，p)=(n，p)=(m+n，p)=1，n是偶數，則[m：p]＋[n：p]＝[m+n：p]。

24. 如果(m，p)=(m，q)=(m，p－q)=1，p和p-q同為偶數或奇數，則[m：p]－[m：q]＝
    [m：p－q]。

25. 如果m是偶數，則[m：p]不可拆離成[m：q]＋[m：p－q]，則m不是偶數。

26. 如果(m，p)=(m，q)=(m，p－q)=1，q是偶數，則[m：p]－[m：q]＝[m：p－q]。

27. 如果m是大於2的質數，q是偶數且m＞p＞q，則[m：p]－[m：q]＝[m：p－q]。

28. 如果(m，p)=(n，p)=(m－n，p)=1，m 和m－n同是偶數或奇數，則[m：p]－[n：p]＝[m-n：p]。

29. 如果p是偶數，則[m：p]不可拆離成[n：p]－[m－n：p]。

30. 如果(m，p)=(n，p)=(m－n，p)=1，n是偶數，則[m：p]－[n：p]＝[m－n：p]。

31. 如果p是大於2的質數，n是偶數且p＞m＞n，則[m：p]－[n：p]＝[m－n：p]。

參考資料：

新泰國中83學年度校內科展數學類第一名(撞球台上的數學)，榮獲北縣第35屆科展數學類優等獎，作者：鐘尹君(就讀中央大學)，劉俊良(就讀中興大學)，王子欣(就讀中興大學)，張書誠(就讀台灣師範大學)。 指導老師:李信昌老師

Copyright ©1999~2004昌爸工作坊 all rights reserved